Common Data Structures operations

by · Published · Updated

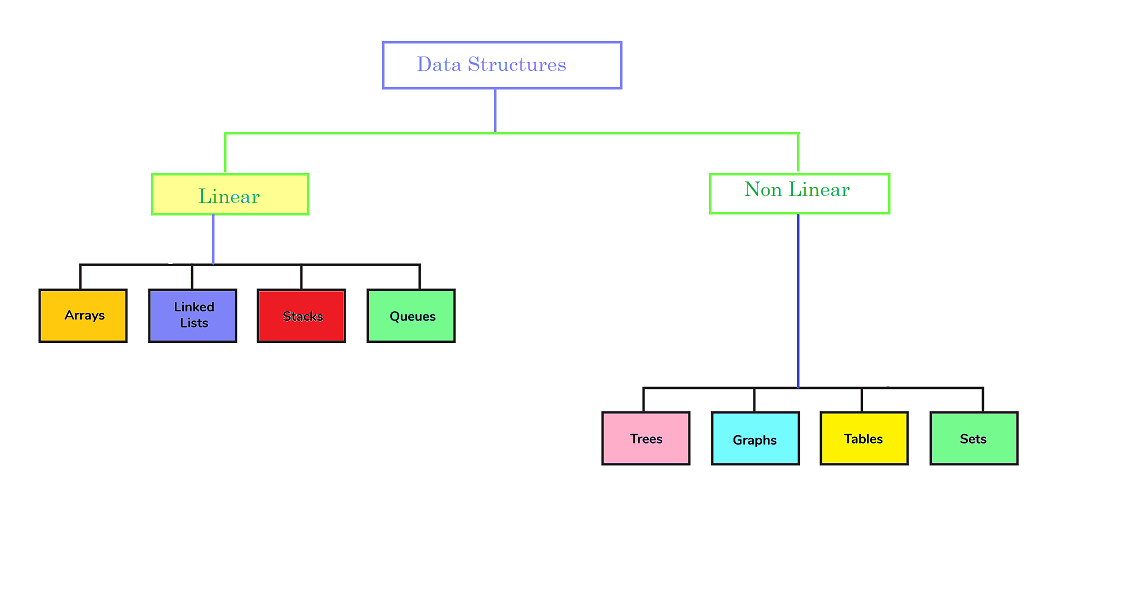
In this article, we learn Common Data Structures operations.  Data Structure is the method of storing data within memory on a computer, to be used quickly and effectively. There are various data structures that can be that are used to store data. It is also defined as the mathematical or logical representation of a specific arrangement for data elements. The representation of a specific data structure within the memory of a machine can be described as a storage structure. Examples: Array, Stack, Queue, Tree, Graph, etc.

Common Data Structures operations

There are many kinds of operations that could be executed to manipulate the data within every data structure. Certain operations are described and illustrated in the following:

  • Traversing The act of traversing data Structure is to go to the elements that are stored within it. It browses the data in a systematic way. It can be accomplished by any DS.
    Below is the program that will demonstrate traversal within an array, queue, stack, and LinkedList
// Java program to traversal in an array
 
import java.util.*;

    class GFG{

        // Driver Code
        public static void main(String[] args)
        {
            // Initialise array
            int arr[] = { 1, 2, 3, 4 };

            // size of array
            int N = arr.length;

            // Traverse the element of arr[]
            for (int i = 0; i < N; i++) {

                // Print the element
                System.out.print(arr[i] + " ");
            }

        }
    }

Below is the program to illustrate traversal in a Stack:

class GFG{

    // Function to print the element in stack
    static void printStack(Stack<Integer> St)
    {

        // Traverse the stack
        while (!St.isEmpty()) {

            // Print top element
            System.out.print(St.peek() +" ");

            // Pop top element
            St.pop();
        }
    }

    // Driver Code
    public static void main(String[] args)
    {
        // Initialise stack
        Stack<Integer> St = new Stack<>() ;

        // Insert Element in stack
        St.add(4);
        St.add(3);
        St.add(2);
        St.add(1);

        // Print elements in stack
        printStack(St);
    }
}

 

  • searching: Searching is the process of finding an element within the specified data structure. It is considered successful when the element that is required is located. The search is an operation that can be carried out on data structures like linked lists, array graphs, trees, graphs, and so on.
    Below is the program that will demonstrate searching for an element in an array of the stack, queue, or LinkedList:
#include <iostream>
using namespace std;

// Function that finds element K in the
// array
        void findElement(int arr[], int N, int K)
        {

        // Traverse the element of arr[]
        // to find element K
        for (int i = 0; i < N; i++) {

        // If Element is present then
        // print the index and return
        if (arr[i] == K) {
        cout << "Element found!";
        return;
        }
        }

        cout << "Element Not found!";
        }

// Driver Code
        int main()
        {
        // Initialise array
        int arr[] = { 1, 2, 3, 4 };

        // Element to be found
        int K = 3;

        // size of array
        int N = sizeof(arr) / sizeof(arr[0]);

        // Function Call
        findElement(arr, N, K);
        return 0;
        }

 

  • Insertion The operation that we use on all data structures. Insertion refers to the addition of an element within the data structure. Insertion is effective when the required element has been added to the needed data structure. It fails in certain instances when the data structure is large and there is no space within the structure to include any additional elements. In addition, the insertion can be described by identical names as insertion into the structure such as linked-list, array graph, or tree. In stack, this action is known as Push. In queue this operation is known as Enqueue.
    Below is the program that will show the insertion of arrays as well as queue, stack and LinkedList:
#include <iostream>
using namespace std;

// Function to print the array element
        void printArray(int arr[], int N)
        {
        // Traverse the element of arr[]
        for (int i = 0; i < N; i++) {

        // Print the element
        cout << arr[i] << ' ';
        }
        }

// Driver Code
        int main()
        {
        // Initialise array
        int arr[4];

        // size of array
        int N = 4;

        // Insert elements in array
        for (int i = 1; i < 5; i++) {
        arr[i - 1] = i;
        }

        // Print array element
        printArray(arr, N);
        return 0;
        }

 

  • deletion: It is the operation we use on all data structures. Deletion is the process of removing elements from the data structure. The deletion operation is completed when the needed element is removed from the structure. The deletion shares the same title as a deletion in the data structure in the form of an array or linked-list graph, tree, etc. On a stack, this action is known as Pop. In Queue this is referred to as Dequeue.
    Below is the code to show dequeue within Stack, Queue, and LinkedList

Another method :

Create: –
It stores memory for programs by declaring the elements. The development of a data structure
It is possible to do this at any time during

  1. Compile-time
  2. Run-time.

You can utilize the malloc() function.

Selection:-
It chooses specific data from the data. You can select any specific data by putting a condition in the loop.

Update
It changes the data in its data structures. It can also update particular data by setting conditions in a loop, such as the select method.

Sort
Sorting data according to a certain order (ascending or descending).
We can use the aid of a variety of sorting algorithms to sort data with less time. Examples: bubble sort, which requires O(n^2)time to separate data. There are many algorithms in use including merge sort, insertion type, quick sort, selection sort, etc.

Merge
The merging of data from two different orders within the same order could either ascend or descend. We employ merge sort to join sorting data.

Split Data
Separating data into various parts to allow the process to be faster and more efficient.

 

Read More:-

 

Tags:

You may also like...